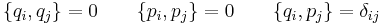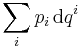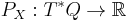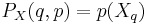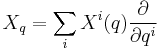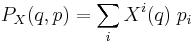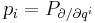Canonical coordinates

In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics. As Hamiltonian mechanics is generalized by symplectic geometry and canonical transformations are generalized by contact transformations, so the 19th century definition of canonical coordinates in classical mechanics may be generalized to a more abstract 20th century definition in terms of cotangent bundles.

This article defines the canonical coordinates as they appear in classical mechanics. A closely related concept also appears in quantum mechanics; see the Stone-von Neumann theorem and canonical commutation relations for details.

1 Definition, in classical mechanics
2 Definition, on cotangent bundles
3 Formal development
4 Generalized coordinates
5 See also
6 References

Definition, in classical mechanics

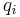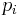In classical mechanics, canonical coordinates are coordinates $q_i\,$ and $p_i\,$ in phase space that are used in the Hamiltonian formalism. The canonical coordinates satisfy the fundamental Poisson bracket relations:

$\{q_i, q_j\} = 0 \qquad \{p_i, p_j\} = 0 \qquad \{q_i, p_j\} = \delta_{ij}$

Canonical coordinates can be obtained from the generalized coordinates of the Lagrangian formalism by a Legendre transformation, or from another set of canonical coordinates by a canonical transformation.

Definition, on cotangent bundles

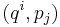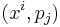Canonical coordinates are defined as a special set of coordinates on the cotangent bundle of a manifold. They are usually written as a set of $(q^i,p_j)$ or $(x^i,p_j)$ with the x 's or q 's denoting the coordinates on the underlying manifold and the p 's denoting the conjugate momentum, which are 1-forms in the cotangent bundle at point q in the manifold.

A common definition of canonical coordinates is any set of coordinates on the cotangent bundle that allow the canonical one form to be written in the form

$\sum_i p_i\,\mathrm{d}q^i$

up to a total differential. A change of coordinates that preserves this form is a canonical transformation; these are a special case of a symplectomorphism, which are essentially a change of coordinates on a symplectic manifold.

In the following exposition, we assume that the manifolds are real manifolds, so that cotangent vectors acting on tangent vectors produce real numbers.

Formal development

Given a manifold Q, a vector field X on Q (or equivalently, a section of the tangent bundle TQ) can be thought of as a function acting on the cotangent bundle, by the duality between the tangent and cotangent spaces. That is, define a function

$P_X:T^*Q\to \mathbb{R}$

such that

$P_X(q,p)=p(X_q)$

holds for all cotangent vectors p in 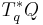$T_q^*Q$ . Here, 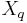$X_q$ is a vector in 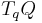$T_qQ$ , the tangent space to the manifold Q at point q. The function 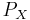$P_X$ is called the momentum function corresponding to X.

In local coordinates, the vector field X at point q may be written as

$X_q=\sum_i X^i(q) \frac{\partial}{\partial q^i}$

where the 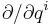$\partial /\partial q^i$ are the coordinate frame on TQ. The conjugate momentum then has the expression

$P_X(q,p)=\sum_i X^i(q) \;p_i$

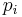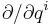where the $p_i$ are defined as the momentum functions corresponding to the vectors $\partial /\partial q^i$ :

$p_i = P_{\partial /\partial q^i}$

The 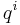$q^i$ together with the 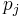$p_j$ together form a coordinate system on the cotangent bundle 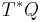$T^*Q$ ; these coordinates are called the canonical coordinates.

Generalized coordinates

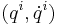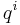In Lagrangian mechanics, a different set of coordinates are used, called the generalized coordinates. These are commonly denoted as $(q^i,\dot{q}^i)$ with $q^i$ called the generalized position and 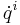$\dot{q}^i$ the generalized velocity. When a Hamiltonian is defined on the cotangent bundle, then the generalized coordinates are related to the canonical coordinates by means of the Hamilton–Jacobi equations.

References

see H. Goldstein